triadalong.blogg.se

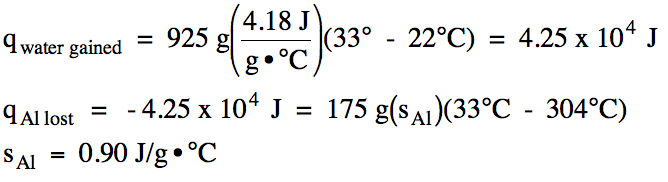
Δ S univ = Δ S sys + Δ S surr = Δ S sys + As a result, q surr is a good approximation of q rev, and the second law may be stated as the following:

For example, combustion of a fuel in air involves transfer of heat from a system (the fuel and oxygen molecules reactants) to surroundings that are infinitely more massive (the earth’s atmosphere). In such cases, the heat gained or lost by the surroundings represents a very small, nearly infinitesimal, fraction of its total thermal energy. Nonspontaneous (spontaneous in opposite direction)įor many realistic applications, the surroundings are vast in comparison to the system. The Second Law of Thermodynamics Δ S univ > 0 A summary of these three relations is provided in Table 1. These results lead to a profound statement regarding the relation between entropy and spontaneity known as the second law of thermodynamics: all spontaneous changes cause an increase in the entropy of the universe. This process involves no change in the entropy of the universe. In this case, the system and surroundings experience entropy changes that are equal in magnitude and therefore sum to yield a value of zero for Δ S univ. The temperature difference between the objects is infinitesimally small, T sys ≈ T surr, and so the heat flow is thermodynamically reversible.This process involves a decrease in the entropy of the universe. The magnitude of the entropy change for the surroundings will again be greater than that for the system, but in this case, the signs of the heat changes will yield a negative value for Δ S univ. The arithmetic signs of q rev denote the gain of heat by the system and the loss of heat by the surroundings. Again designating the hotter object as the system and invoking the definition of entropy yields the following: This is never observed to occur spontaneously. The objects are at different temperatures, and heat flows from the cooler to the hotter object.This process involves an increase in the entropy of the universe. Since T sys > T surr in this scenario, the magnitude of the entropy change for the surroundings will be greater than that for the system, and so the sum of Δ S sys and Δ S surr will yield a positive value for Δ S univ. The arithmetic signs of q rev denote the loss of heat by the system and the gain of heat by the surroundings. Designating the hotter object as the system and invoking the definition of entropy yields the following: The objects are at different temperatures, and heat flows from the hotter to the cooler object.There are three reasonable possibilities for such a process: To illustrate this relationship, consider again the process of heat flow between two objects, one identified as the system and the other as the surroundings. In thermodynamic models, the system and surroundings comprise everything, that is, the universe, and so the following is true:

By expanding consideration of entropy changes to include the surroundings, we may reach a significant conclusion regarding the relation between this property and spontaneity. Processes that involve an increase in entropy of the system (Δ S > 0) are very often spontaneous however, examples to the contrary are plentiful. In the quest to identify a property that may reliably predict the spontaneity of a process, we have identified a very promising candidate: entropy. | Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises | The Second Law of Thermodynamics